This is a facilitator’s guide for The Long COVID Game, an instructional game on the cumulative probability of Long COVID.
Overview
This short (<5min) instructional game can help illustrate the cumulative probability of Long COVID. It was designed for large groups, such as a classroom of students. The goal is to communicate the benefits of wearing a respirator, such as an N95, to reduce the number of COVID infections and thus the risk of contracting Long COVID.
Disclaimer
The Long COVID Game is what’s known as a persuasive game—the goal here is to persuade participants to wear a respirator based on the cumulative probability of acquiring Long COVID on a population level. While the risk of contracting Long COVID is approximately 15%/COVID infection, the game treats the cumulative probability (1 infection = 15%; 2nd infection = 25%; 3rd infection = 38%) as the risk of subsequent infections. I explain the pedagogical reason for this design decision below in the ‘Design Rationale’ section.
Setup
Inform your audience that they will be playing a short game called The Haunted Woods. Try not to frame the exercise as a learning game or a COVID safety game; such priming can interfere with the learning outcomes here.
Participants will need to generate a random number between 1-10 to play. If they have a phone, tablet, laptop, or desktop they can use Google to generate a random number or use this shortened link: bit.ly/roll10. If you have a projector, you might help set the scene with a dark, slightly unnerving image of a forest like the one below.

Instructions
1) Read the following preface: “In a far away land, there are three villages surrounded by a a sprawling forest. Once the forest was lush and vibrant, but it has grown dark and gloomy of late. The villagers have taken to calling it The Haunted Woods and all who pass through it become cursed. But pass through it they must, for once every year the villagers need to make a pilgrimage to the The Sacred Well and return with its life-giving waters. In time the curse will fade into nothing, but some are not so fortunate…”
“You are in the first village and have returned with your fellow villagers from the first pilgrimage since the woods became haunted and cursed all those who enter…”
2) Have participants roll a random number between one and ten. Inform those who rolled two or less that while the other villagers will recover from being cursed, their curse is permanent. Tell them to make a note of each village/round in which they are permanently cursed.
3) Read the following prompt: “You are now in the second village. A year has passed and it is time for the villagers to take the pilgrimage once again.”
Have participants roll a random number between one and ten. Inform those who rolled three or less that while the other villagers will recover from being cursed, their curse is permanent. Remind them to make a note of each village/round in which they are permanently cursed.
4) Read the following prompt: “You are now in the third village. Another year has passed and it is time for the villagers to take the pilgrimage once again.”
Have participants roll a random number between one and ten. Inform those who rolled four or less that while the other villagers will recover from being cursed, their curse is permanent.
5) After the third round, read the following: “After years of being cursed, a village healer has made a powerful discovery about The Haunted Woods, producing a magic ward that repels the curse for all those who choose to wear it. Could this cursed era finally be at an end?”
6) Ask all participants who became permanently cursed in the first village to raise their hands. Inform them that, unfortunately, these are the same number of people who develop Long COVID after one infection. Then ask those cursed in the second village to raise their hands; these are the same number of people who have Long COVID after two infections. Finally, have the participants who became permanently cursed in the third village raise their hands; inform them that these are the same number of people who have Long COVID after three or more infections.
7) Inform participants that the numbers here have been rounded slightly to work with a ten sided die. As reported by Statistics Canada, 15% of those who have been infected once report Long COVID symptoms; that number increases to 25% after 2 infections; 38% after 3+ infections. Meanwhile, the magic ward that blocks the curse represents a respirator, such as an N95, which reduces exhaled viral load by upwards of 98%.
8) Finally, note that when playing the game, it would be absurd for the villagers not to wear the ward against the curse. So, why not wear a respirator?
Additional Notes
- If possible, provide N95 masks for attendees distributed after the exercise. In my case, I approached each table and said: ‘Can I offer you a free, high-quality N95 mask?’ This proved quite effective.
- Consider how you contextualize the exercise afterwards. I made it clear to my students that ‘This is not coming from me, Steve, your game design prof. This is coming from someone who cares about your well-being and genuinely wants the best for you and your health. I don’t want Long COVID to impact your studies, your future prospects, or any part of your life.’
- Leverage additional resources as you see fit. I included additional information on the current rate of transmission, the physics of N95 respirators, the state of local healthcare, and the multi-organ impact of Long COVID (see below for links/references).
- Inform, don’t alarm. The goal here is not to alarm or scare your audience into wearing respirators. Instead, we are using game-based learning and situated learning theory to establish the context in which certain outcomes, actions, and choices become probable and reasonable. We then make the connection from the game to everyday life. Since the cumulative probability remains the same, participants intuitively understand the growing number of Long COVID cases if the curse/virus continues to spread (evidenced by the number of players who are permanently cursed in the third village). This helps establish a tangible context for the value of the ward/respirators (the villagers would be foolish not to wear the magic ward, so too would participants be unwise not to wear an N95).
Design Rationale
As noted in the disclaimer above, this game treats the growing cumulative probability of being permanently cursed/developing Long COVID as the risk per individual curse/infection. I made this decision to shift the game away from individual risk to represent a population as a whole. From a learning game design perspective, there’s a compelling reason why you might not want to try & illustrate this via 15% chance of LC per infection (i.e. a 3 or less on a 20-sided die): luck.
While the cumulative effect of 15% chance of LC/infection will emerge in the long run, in a time-limited session with truly random numbers you might not see that distribution. From a learning game design perspective, we have to assume that at least some players will not spend a prolonged time with the game or that the time constraints of a classroom limit the amount of time needed to control for randomness and let the probabilities play out.
The fact is, focusing on individual risk and thus 3/20 chance of being permanently cursed will invariably result in some players ‘beating the odds’ and having a diminished sense of risk. I don’t think this is a responsible approach given the possibility of this outcome and the time constraints involved for learning games. Indeed, such a game might end out counteracting the learning outcomes, teaching ‘lucky’ players that the risk is negligible.
To offset this possibility, several design decisions were made. In the fictional scenario we encounter villagers who are all cursed once a year; all villagers go on multiple pilgrimages where they are cursed again; and we treat the cumulative probability of being permanently cursed in each successive round as the risk to the population (e.g. it assumes that out of a population of a 100 villagers, 15 are permanently cursed by the end of the first round, 25 by the end of the second round, etc., regardless of each participants roll in the preceding round).
In actuality, various factors—including individual behaviour, socio-economics, number of vaccinations, etc.—factor into your risk of acquiring COVID. And at an individual level, your risk of developing Long COVID remains around 15%/infection, or 3 or less on a 20-sided die. But at the population level, we would still see a growing number of those permanently cursed/acquiring Long COVID over time.
My primary audience in designing the game was university students where one COVID infection/year can be seen as normal and even reasonable. But by third year, a cohort of a 100 students that has been infected every year of their undergrad could see as many as 38 of those students struggling with Long COVID. That possibility seems completely unacceptable to me. And so the game controls for randomness, hence why in the third round of the game players roll against the cumulative probability with a 4 or less resulting in a permanent curse.
Finally, while you could create a comprehensive simulation for individual risk of contracting Long COVID (I have thought of doing that many times over the past four years), the potential for ‘lucky’ players to come away with a diminished impression of the risk of Long COVID is, in my mind, too high. Instead, focusing on the cumulative risk at the population level seemed like the best compromise for a responsible learning game on the topic.
Instructional Resources
I showed this short video on the science of N95 respirators to my students to clarify any misconceptions about how they work and why they are very different from surgical and cloth masks.
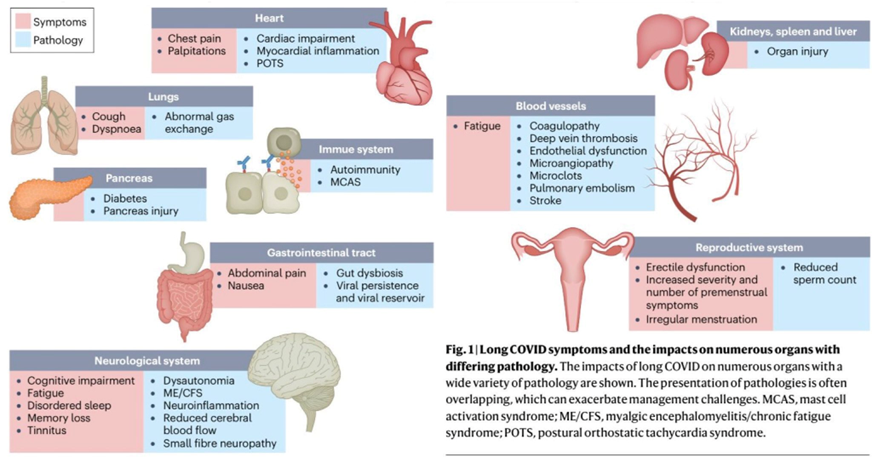
I also used the image below to demonstrate the distributed impact of Long COVID on the body.
Revisions
The scenario above was revised to reflect that while the risk of contracting COVID with each infection is approximately 15%, the cumulative probability means the number of those infected who develop Long COVID increases quite dramatically as the population is repeatedly infected.